VAA(Vertical Approach Angle)とはホームベース上における垂直方向に対する入射角度の事です。
日本語で「バーティカル アプローチ アングル」と言い、4シームにおいて空振りが奪いやすいかどうかの目安になります。
下記の拡大図内の緑色の角度の事です。
.jpg)
VAA(Vertical Approach Angle)の解説
地面と水平を0°と定義されており、このVAAが0°に近ければ近いほど(地面と水平に近いほど)、4シームにおいて空振りが奪いやすいという傾向が出ています。
なお、VAAはマイナスが標準です。
計算式
- VAA = – arctan( Vz / Vy ) ×( 180 / π )
*Vzはホームベース到達時の落下方向の速度
*Vyはホームベース到達時の速度
z軸(落下方向)とy軸(投球方向)の2つ終速からアークタンジェントで角度を求めるだけです。
baseballsavantのデータに50feet到達時点での各軸の速度と加速度のデータがあります。
加速度一定と仮定すれば、各軸の終速が計算できますので、VAA・HAA共に計算ができます。
計算が面倒な方向けに線形回帰分析で得られた近似式を作成したのでご活用ください。
- VAA= -11.5748 +(0.0371 × pfx_z)+(0.0347 × plate_z)+(0.0570 × release_speed)-(0.0351 × release_pos_z)-(0.0001 × release_extension)
*pfx_z:縦変化量(cm)
*plate_z:投球高さ(cm)
*release_speed:球速(km/h)
*release_pos_z:リリース高さ(cm)
*release_extension:エクステンション(cm)
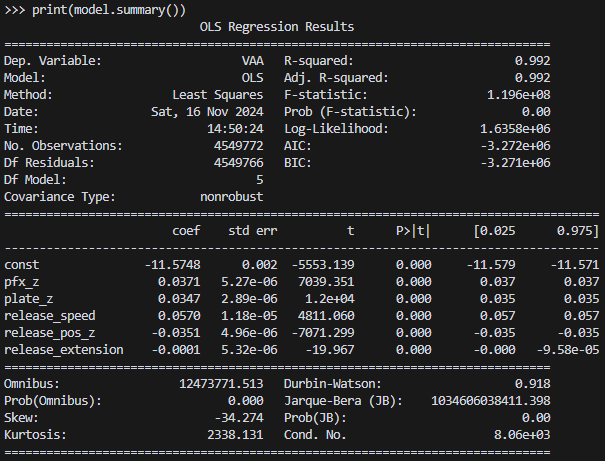
線形回帰分析の詳細を貼っておきます。
R-squaredが0.992なので上記の近似式でVAAの99.2%を説明できている事がわかります。
MLB平均値【2018~2024】
下記は2018~2024年MLBの4シームの各平均値です。
| 年 | 球速 (km/h) |
縦変化 (cm) |
リリース高 (cm) |
投球高 (cm) |
VAA (°) |
Whiff% |
| 2018 | 149.9 | 39.8 | 179.9 | 80.8 | -5.10 | 20.5 |
| 2019 | 150.3 | 39.7 | 181.0 | 82.4 | -5.06 | 21.6 |
| 2020 | 150.2 | 40.6 | 179.5 | 82.9 | -4.96 | 22.5 |
| 2021 | 150.8 | 41.0 | 180.5 | 83.6 | -4.93 | 22.0 |
| 2022 | 151.2 | 41.1 | 179.1 | 85.6 | -4.80 | 21.8 |
| 2023 | 151.6 | 39.9 | 177.7 | 85.8 | -4.78 | 22.2 |
| 2024 | 151.7 | 39.9 | 177.4 | 86.8 | -4.73 | 21.8 |
2018年に平均-5.10°だったVAAですが、2024年には-4.73°となっており、年々0°に近づいている事がわかります。
VAAに影響する主な変数は近似式の通り、球速・縦変化量・リリース高さ・投球高さです。
これらがVAAを0°に近づけるように年々変化をしています。
特に影響の大きい投球高さは、この7年で6cm、ボール1個分弱高くなっています。
MLBランキング【2024】
2024年MLBの4シームVAAランキングを紹介しておきます。対象は200球以上を投げている選手です。
| 順位 | 選手 | 球速 (km/h) |
縦変化 (cm) |
リリース高 (cm) |
投球高 (cm) |
VAA (°) |
Whiff% |
| 1位 | Tim Hill | 146.0 | 10.3 | 103.7 | 92.3 | -3.33 | 19.7 |
| 2位 | Paul Sewald | 147.0 | 34.3 | 135.0 | 94.0 | -3.37 | 24.3 |
| 3位 | Alexis Díaz | 151.2 | 33.3 | 138.5 | 92.3 | -3.41 | 23.7 |
| 4位 | Edwin Uceta | 151.6 | 36.7 | 140.5 | 88.8 | -3.51 | 36.6 |
| 5位 | Craig Kimbrel | 151.0 | 39.4 | 144.7 | 88.2 | -3.57 | 28.9 |
| 6位 | Edwin Díaz | 156.9 | 33.5 | 146.4 | 89.4 | -3.60 | 36.6 |
| 7位 | Yimi García | 155.3 | 38.1 | 156.8 | 95.7 | -3.61 | 31.7 |
| 8位 | Joe Ryan | 151.3 | 35.2 | 144.5 | 88.4 | -3.71 | 27.5 |
| 9位 | Nick Sandlin | 149.0 | 30.6 | 141.8 | 92.8 | -3.71 | 17.8 |
| 10位 | Rafael Montero | 153.5 | 39.9 | 156.5 | 92.0 | -3.74 | 24.6 |
| 44位 | 今永昇太 | 147.5 | 46.5 | 166.2 | 89.1 | -4.17 | 17.5 |
| 133位 | ダルビッシュ | 151.3 | 42.5 | 171.8 | 83.1 | -4.60 | 15.1 |
| 151位 | 山本由伸 | 153.7 | 39.5 | 167.3 | 77.4 | -4.64 | 17.6 |
| 参考 | MLB平均 | 151.7 | 39.9 | 177.4 | 86.8 | -4.73 | 21.8 |
変則系で低いリリースポイントの投手が上位にランクインしています。
また、投球高さは90cmを超えてくる投手も多くランクインしています。(ストライクゾーンは下限45.7cm、真ん中76.2cm、上限106.7cm)
Whiff%(スイング時の空振り率)はMLB平均の22%前後を超える選手が多くなっています。
ただし、VAAが1位のTim HillのWhiff%が平均以下であることから、必ずしもVAAが0に近くなれば空振り率が高くなるわけではないことがわかります。
あくまでも目安として見て頂くのが良いでしょう。
VAAの改善
各変数の影響度は先ほどの近似式を見るとわかりやすいです。
- VAA= -11.5748 +(0.0371 × pfx_z)+(0.0347 × plate_z)+(0.0570 × release_speed)-(0.0351 × release_pos_z)-(0.0001 × release_extension)
*pfx_z:縦変化量(cm)
*plate_z:投球高さ(cm)
*release_speed:球速(km/h)
*release_pos_z:リリース高さ(cm)
*release_extension:エクステンション(cm)
0に近づけるようにすると空振りが奪いやすくなります。
0に近づけるためには
- ホップ量を多く
- 投球高さを高くし
- 球速を速く
- リリース高さを低くする
と良い事がわかります。
式の傾きでVAAの各変数の影響度がわかります。
- ホップ量 → × 0.0371
- 投球高さ → × 0.0347
- 球速 → × 0.0570
- リリース高さ → × -0.0351
- エクステンション → × -0.0001
エクステンションの傾きはほぼ0なので無視できます。
リリース高さはマイナスの傾きなので低いほど良いわけですが、投球フォームを変更するのはリスクがあります、、、、
球速を10km/h速くすると、10×0.057なので0.57°の改善となりますが、なかなか難しいですね。
ホップ量を10cm大きくすると、10×0.0371なので、0.371°の改善となりますが、これも難しいです。
投球高さを10cm高くすると、10×0.0347なので、0.347°の改善となります。これなら誰にでも可能です。
20cmであれば0.694°、30cmであれば1.041°となるので、投球高さでVAAを大きく改善できることがわかります。
なので、VAAを改善したい場合は投球高さを意識しましょう。
空振りへの影響度
下記の私の投稿は機械学習のWhiff%(スイング時の空振り率)予測モデルの各変数の影響度を計算した結果を投稿したものです。
baseballsavantのデータから機械学習でwhiff%(スイングの際の空振り率)を予測する学習モデルを作成して各変数の重要度を出すとこんな感じ
■重要度順位
①:投球場所
②:変化量
③:リリース位置
④:球速*この予測学習モデルはど素人の私が作成したものなのであくまでも参考までに https://t.co/asRAK81cBO pic.twitter.com/94lyNYUilN
— ひろ@野球 (@yuki_scope) May 22, 2023
続いて予測モデルの変数にVAAを入れて各変数の影響度を出してみると下記に。
ちなみに変数を変えてみるとこんな感じ
VAA(vertical approach angle)に引っ張られて他変数の影響度が下がる
これはwhiff%の予測の多くの部分をVAAで説明できるからです
AVVは球速・投球高さ・ホップ量・リリース高さ・珠持ちを変数としています
詳しくは下記でhttps://t.co/W1f0k9xDbt https://t.co/wsbYaMRlGW pic.twitter.com/keuQOYUIOj— ひろ@野球 (@yuki_scope) May 22, 2023
VAAの影響度が圧倒的に強く、空振り予測の多くをVAAで予測できてしまうという結果になりました。
先ほどの近似式を見て頂くとわかる通り、VAAには空振りを奪えるかどうかを左右する変数が盛り込まれています。
なので当然の結果と言えます。
まとめ
VAAは4シームで空振りを奪いやすいかどうかの目安になる指標で、投球高さである程度の制御が出来るので、どんな投手でも意識できます。
「4シームで空振りが奪えない」「4シームで空振りが奪いたい」という投手は投球高さを意識した投球を実践してみましょう。
*本文では触れていませんが、変化球においてはVAAの重要度は高くなく、特に気にする必要はありません。


とは?-120x68.jpg)
-120x68.jpg)
コメント